In this post I want to cover how you put windows into a building or find the next one on a long line of telegraph poles. There is some geometrical construction but not I hope much more than joining up dots. The there is certainly no algebra! Poor perspective is one of the most common faults in paintings either painted from imagination or life. Unfortunately any viewer will feel that something is wrong even if they don’t quite know why it doesn’t quite work. These little tutorials are aimed at painters or other artists who need to get it right enough to make the viewer comfortable with what they see not really for architects who need to get things spot on. To this end I am starting as simply as possible. I am assuming the reader knows the absolute basics such as lines join up at the horizon at what is usually termed the vanishing point and that the horizon is always at the viewer’s eye level. I will cover these very basic topics in the future but not in these posts. I am doing the first section in a back to front way in that I am starting with a row of telegraph poles and then showing why they are in the places they are and the basic principles that caused them to appear in those positions. So, off we go.
.

Here is the only geometric construction we are going to use in this tutorial. If you draw a diagonal cross from corner to corner (the red lines) of a square or rectangle then they will cross at the middle point. If you draw the green lines through that middle point then it will divide the original shape into identical quarters. The blue line shows that you could do this again and again chopping the rectangle into ever smaller pieces. If you think of the black rectangle as a window opening then the green line might be the window bars separating the glass panes.
.

So here are our telegraph poles evenly spaced running off to the horizon. You can clearly see they get smaller as they get further away and the spaces between them get narrower too. But what exactly controls why each pole is in the place where it looks right to the eye. I have made a black mark on each pole which is halfway up. So next we will draw some lines over the picture to find out.
.

First thing is to mark the Horizon with the blue line. The Horizon is always at eye level. If you are painting outside then if you hold a brush horizontally close in front of your eyes it will lie along the horizon. If you are working from a photo, say of buildings, then if you find a window ledge or other level feature that is aligned with the top or bottom of the picture and neither slopes up nor down then that is also the horizon. You can also join up the tops and bottoms of features such as the poles above to find where they meet and that is once again the horizon level.
.

Here I have done just that with the black lines. We learn something else from this as well and that is the Vanishing Point which defines where all the tops and bottoms of our poles is. Next we use the Geometry rules in the first diagram to see what is going on.
.

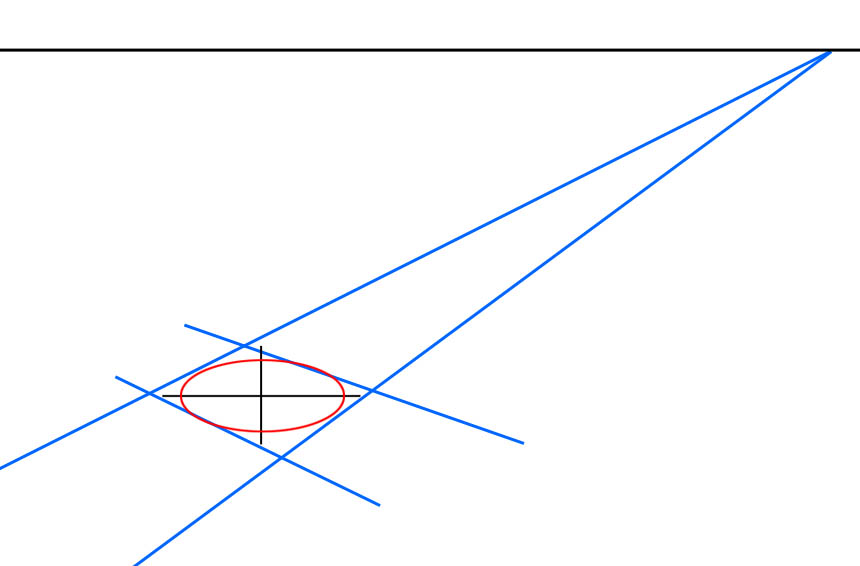
Here I have drawn a red line through all the centres, note it also meets at the horizon an all horizontal lines will always do. Then as in the first Diagram I have added a blue cross. As you would expect the lines cross on on the red line. If you wanted to add a post exactly between the first two where the blue lines cross is where it would go.
.

Now here is the clever bit. Look at where the green line goes. Because three posts together make a big rectangle with the second post in the middle the green line will always cross at the middle of the second pole. This means that even if we only have the first two poles in our drawing we can find the right place for the third pole, it is always where the green line hits the top black line. Once we have the second and third pole we can then use them to find the fourth pole and so on until they are too small to see.
.

Here I have drawn a few of them in to show that it really will carry on finding the pole positions until the horizon, though I would start guessing long before that. In the next part I will show how you use these very basic methods to put windows into a building. If anyone finds anything unclear please comment and I will either answer the query in a comment or update the post if others have the same difficulty.
Part 2 is here.


 Here is the plan of a simple set up, as before the green triangle marks our viewpoint. We often get rows of things receding from us, looking down a romanesque church nave would be an example. Below is how traditional two point perspective renders the scene.
Here is the plan of a simple set up, as before the green triangle marks our viewpoint. We often get rows of things receding from us, looking down a romanesque church nave would be an example. Below is how traditional two point perspective renders the scene.